Katsoin Juhan ja Saulin mielenkiintoisen videokatsauksen mallisalkun kymmenvuotiseen historiaan ja tuottoihin. Videosta syntyi idea tutkia mallisalkun tuottoja kvantitatiivisin menetelmin. Sain kuukausituottodatan Verneriltä (kiitokset siitä!), joten tein analyysini ja ajattelin laittaa sen tänne muidenkin nähtäväksi. Kaikki mahdolliset virheet ovat omiani ja kehotankin suhtautumaan tuloksiin terveellä skeptisyydellä.
Dataa on tasan kymmenen vuoden ajalta eli 120 kuukausituottoa väliltä kesäkuu 2011 – toukokuu 2021.
Yritän analyysissä vastata näihin kysymyksiin:
-
Mitkä rahoitustutkimuksesta tutut riskifaktorit selittävät mallisalkun tuottoja ja selittyykö mallisalkun suuri tuotto riskifaktoreilla eli sijoitustyylillä?
-
Mikä on paras (mallisalkun tuottoja ja riskejä parhaiten kuvaava) vertailuindeksi?
-
Onko mallisalkulla tilastollisesti merkittävää ylituottoa (alfaa) kun mallisalkun tuotot selitetään vertailuindeksin tuotoilla?
-
Onko mallisalkulla tilastollisesti merkittävää ylituottoa, jos huomioidaan indeksin lisäksi videollakin mainitut mallisalkun paras osake Revenio tai parhaat neljä osaketta?
-
Mistä pääkomponenteista mallisalkun tuotto muodostuu?
-
Kuinka suurella riskillä mallisalkun tuotto on saavutettu?
-
Osakepaino on ollut reilusti alle 100%. Miten ja millaisella riskillä salkku olisi tuottanut suuremmalla osakepainolla?
-
Onko tuotto ja mahdollinen ylituotto ollut taitoa vai tuuria?
Korkeat tuotot tulkitaan yleensä automaattisesti osakepoimintataidoksi, mutta todellisuudessa puhdas, riskifaktorikorjattu tai tyylikorjattu, osakepoimintataito on jo akateemisen tutkimuksen valossa hyvin harvinaista. Yleensä, kun tehdään kattava riskifaktorianalyysi, huomataan ettei sijoitustyylin selittämän tuoton jälkeen jää jäljelle merkittävää osakepoimintataitoa.
Hyvä esimerkki on AQR:n kavereiden kuuluisa paperi Buffett’s Alpha. Paperissa näytetään miten Berkshire Hathawayn tuotot on selitettävissä muutamalla riskifaktorilla eli käytännössä sijoitustyylillä: ”Buffett’s returns appear to be neither luck nor magic, but, rather, reward for the use of leverage combined with a focus on cheap, safe, quality stocks.” Mainittakoon, että itse pidän tätä tulosta vielä kunnioitettavampana saavutuksena kuin maagista osakepoimintataitoa: Buffett on tämän tutkimuksen valossa todellinen strategi ja visionääri hyödyntäessään tuottavia sijoitustyylejä hallitulla vivulla jo vuosia ja vuosikymmeniä ennen kuin rahoitustutkimus tunnisti nämä ylituoton lähteet.
Tein jokin aika sitten analyysin myös erittäin hyvin menestyneestä suomalaisesta rahastosta PYN Elite. Tämäkin analyysi osoittaa, että PYN Eliten loistava track record ei ehkä ole syntynyt puhtaasta riskikorjatusta osakepoimintataidosta (alfasta), vaan enemmän oikea-aikaisesta rohkeasta altistumisesta aliarvostetulle ja epälikvidille markkinalle (mikä itsessään tietysti voi olla taitoa siinä missä puhdas osakepoimintataitokin).
Erityisesti Buffett, ja nykyään jossain määrin myös PYN Elite, sijoittaa valtavan suurta ja jatkuvasti kasvavaa pääomaa, jolloin osakepoiminnat kohdentuvat suuriin ja tehokkaasti hinnoiteltuihin yhtiöihin. Puhdas osakepoimintataito megacap -avaruudessa on ymmärrettävästi todella vaikeaa, ellei mahdotonta. Mutta nyt tarkastellaan Inderesin mallisalkkua, joka operoi verrattain pienten ja mahdollisesti epätehokkaammin hinnoiteltujen yhtiöiden kentässä, missä puhdasta riskikorjattua osakepoimintataitoa ehkä voi olla?
Lähdin kokeilemaan rahoitustutkimuksessa löydettyjä riskifaktoreita ja selittämään mallisakun tuottoja niiden avulla. Valitsin alkuun Fama&French 5 faktorin mallin (Euroopan faktorit) ja lisäsin kuudenneksi faktoriksi momentumin. Tällä kattauksella voi selittää tyypillisen osakerahaston tuotot lähes täydellisesti. Eurooppa-faktorit eivät täydellisesti kuvaa Suomen markkinaa, joten kokeilin markkinariski-faktoreina myös OMXHCAPGI (mallisalkun vertailuindeksi) ja OMXHSCGI (Suomen pienyhtiöindeksi) total return (osingot uudelleensijoitettu) indeksejä. Näiden lisäksi käytin AQR:n suomen markkinalle laskettuja faktoreita (sisältäen perusfaktorit size, value ja momentum) ja erityisen lupaavana pitämääni AQR:n quality-minus-junk faktoria (laatufaktori) sekä toista AQR:n lempifaktoreista: betting-against-beta. Ajoin regressioanalyysit näillä kaikilla ja lisäksi tein faktoreista viivästetyt versiot, joilla voidaan todentaa, mikäli sijoitukset ovat niin epälikvidejä, että altistuminen riskifaktoreille tapahtuu kuukauden tai jopa kahden viiveellä (tämä taktiikka toimi PYN Eliten analyysissä ja toimii usein hyvin epälikvideille hedge rahastoille).
Riskittömänä korkona käytin tässä yhteydessä Seligsonin rahamarkkinarahastoa, mutta sen tuoton mentyä negatiiviseksi (helmikuusta 2017 lähtien) nollasin riskittömän koron (simuloiden pankkitalletusta nollakorolla). Riskittömän koron keskiarvoksi tuli huikeat 0.32% per annum.
Faktorianalyysin tulokset? Onnistuin löytämään selittäviä tekijöitä, mutta (lukumääräisesti) paljon vähemmän ja (selitysvoimaltaan) heikompia kuin odotin. Ainoa faktori markkinariskin lisäksi mikä korreloi vahvasti (ja tilastollisesti merkittävästi) mallisalkun kanssa oli Euroopan ja Suomen size faktori. Ei kovin yllättävää, kun mallisalkku tunnetusti sijoittaa lähinnä pieniin yhtiöihin. Myöskään viivästetyt faktorit eivät korreloineet mallisalkun kanssa, eli mallisalkun tuottoja ei voi laittaa ”illiquidity” premiumin piikkiin.
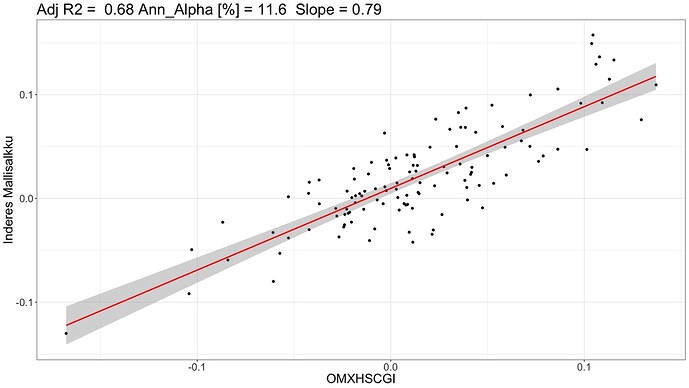
Mikä indeksi selittää mallisalkun tuottoja parhaiten? Selkeä vastaus tähän on Suomen pienyhtiöindeksi OMXHSCGI. Alla olevassa kuvassa nähdään mallisalkun kuukausituotot (y-akseli) selitettynä Suomen pienyhtiöindeksillä (x-akseli).
Mallisalkun OMXHSCGI beta (suoran kulmakerroin) on 0.79 eli 1% muutos indeksissä aiheuttaa keskimäärin 0.79% muutoksen mallisalkun tuotossa. Matala beta heijastelee mallisalkun merkittävää käteispainoa ja mahdollisesti lisäksi keskimäärin alhaisemman betan osakkeita. OMXHSCGI indeksi selittää mallisalkun tuottojen varianssista (riskistä) 68% (R^2 = 0.68) eli 32% mallisalkun riskistä on yhtiökohtaista (idiosynkraattista) riskiä. Yhtiökohtaista riskiä on siis paljon. Selittämätön (yli)tuotto eli alfa (y:n arvo, kun x = 0) on peräti 0.97% per kuukausi, joka on annualisoituna (12*0.97%) 11.6% per vuosi. Ylituotto on tilastollisesti erittäin merkittävä (p-value < 0.001). Malli antaa mallisalkun ylituoton verrattuna markkina-altistukseen (beta) eli verrattuna 0.79*indeksituottoon (ei verrattuna 1*indeksituottoon). OMXHSCGI (malli #3 alla olevassa taulukossa) oli paras malli (suurin R^2) kuvaamaan mallisalkun tuottoja minkä löysin kaikkien faktorimallien joukosta.
Vertailun vuoksi OMXHCAPGI indeksi (malli #1) selittää mallisalkun tuottojen varianssista vain noin 50% eli huomattavasti vähemmän kuin OMXHSCGI. Myös OMXHCAPGI indeksi yhdessä (Euroopan) size faktorin (SMB) kanssa (malli #2) selittää vain noin 53%.
Mallisalkulla on siis erittäin suuri tilastollisesti erittäin merkittävä ylituotto suhteessa sen OMXHSCGI indeksialtistukseen. Mutta onko tämä salkun tähtiosakkeen, Revenion, ansiota? Revenio näyttää mallisalkkuhistorian perusteella olleen mukana käytännössä koko mallisalkun historian ajan. Voin siis ottaa Revenion tuottosarjan (sisältäen osingot ja huomioiden splitit) faktoriksi OMXHSCGI indeksin rinnalle (malli #4). Revenio on tilastollisesti erittäin merkittävä faktori mallisalkun tuotoille kuten odottaa saattaa. Revenion nostaminen faktoriksi nostaa mallin selitysasteen (R^2) 74% tasolle. Myös ylituotto tippuu 0.97% → 0.67% per kuukausi eli 11.6% → 8.0% per annum tasolle. Ylituotto on edelleen todella suuri ja edelleen hyvinkin tilastollisesti merkittävä (p-value < 0.01). Syy miksi ylituotto ei tipu niin paljoa kuin voisi ajatella on, että Revenio itsessään sisältää tuottokomponenttina suurehkon (beta = 1.13) small cap indeksialtistuksen. Eli kun otan Revenion faktoriksi, se pienentää indeksin vaikutusta mallissa, koska osa indeksin vaikutuksesta on nyt Revenio-faktorin sisällä.
Malli #5 on käytännössä sama kuin malli#4. Nyt vain rakennan kuvitteellisen salkun, joka koostuu 0.6338*OMXHSCGI + 0.1363*Revenio kuukausituotoista. Käytän tätä samaa tekniikkaa mallissa #6 ja tässä kohtaa vain tarkistan, että mallit #4 ja #5 antavat samat tulokset eli voin rakentaa kuvitteellisen salkun edellä mainitulla tavalla.
Revenio yksinään OMXHSCGI indeksin kaverina ei siis riitä mihinkään ylituottoa selitettäessä. Entäpä Juhan ja Saulin mainitsemat neljä parasta osaketta yhdessä? Revenio, Talenom, Remedy ja QT OMXHSCGI indeksin rinnalla (malli #6). Tämä on hieman kinkkisempi malli rakentaa, koska kolme viimeksi mainittua osaketta ovat olleet mallisalkussa kohtuullisen lyhyen ajan historian loppupäässä. Rakennan mallin samalla tekniikalla kuin tein mallin #5. Eli jaan historian neljään periodiin: 1: Vain Revenio, 2: Revenio + Talenom, 3: Revenio + Talenom + Remedy ja 4: Revenio + Talenom + Remedy + QT. Ajan jokaiselle periodille regressioanalyysin erikseen ja saan sieltä kunkin osakkeen (ja indeksin) vaikutuksen (betan) mallisalkun tuottoon. Rakennan mallisalkun tuotot regressio-betojen avulla jokaiselle periodille erikseen. Lopuksi yhdistän nämä neljä periodia ja saan tuottosarjan kuvitteelliselle salkulle (malli #6) koko mallisalkun historian ajalta. Tämä malli selittää odotetusti mallisalkun tuotot parhaiten. R^2 on 77%. Ylituotto kutistuu 0.47% per kuukausi eli 5.6% per annum tasolle, mutta on edelleen tilastollisesti merkittävä (p-value < 0.05).
Ylituotto on siis tämän analyysin mukaan edelleen suuri ja tilastollisesti merkittävä vaikka huomioin OMXHSCGI indeksin ja neljä parasta osaketta faktoreina. Ylituottoa on siis tullut paljon myös näiden tähtiosakkeiden ulkopuolelta. 5.6% vuosittainen alfa olisi erinomainen suoritus jo itsessään. Alfa eli selittämätön ylituotto voi pitää sisällään osakepoimintataitoa ja esimerkiksi hyvää ajoittamista. Oikaisen hieman ja oletan analyysissä, että ylituotto muodostuu pääasiassa osakepoimintataidosta.
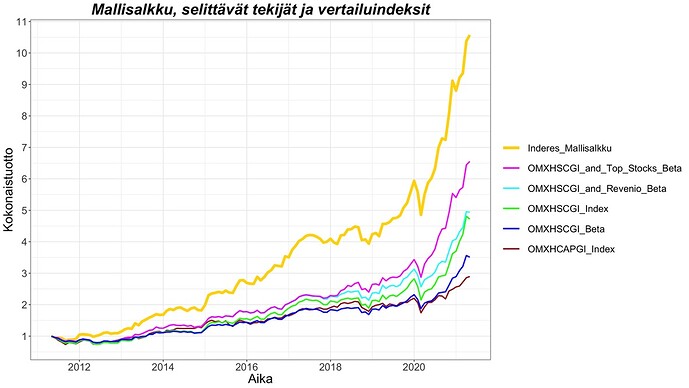
Seuraavassa kuvassa on kumulatiiviset tuotot edellä mainituille portfolioille. ”OMXHSCGI_and_Top_Stocks_Beta” on malli #6 mukainen portfolio, ”OMXHSCGI_and_Revenio_Beta” on malli #5 mukainen portfolio ja uutena portfoliona ”OMXHSCGI_Beta”, joka on mallisalkun OMXHSCGI indeksialtistus (beta), jonka kuukausituotot saadaan kertomalla OMXHSCGI kuukausituotot betalla: 0.7873*OMXHSCGI. Tästäkin kuvasta nähdään silmällä, että mallisalkku erottautuu muista portfolioista selvästi.
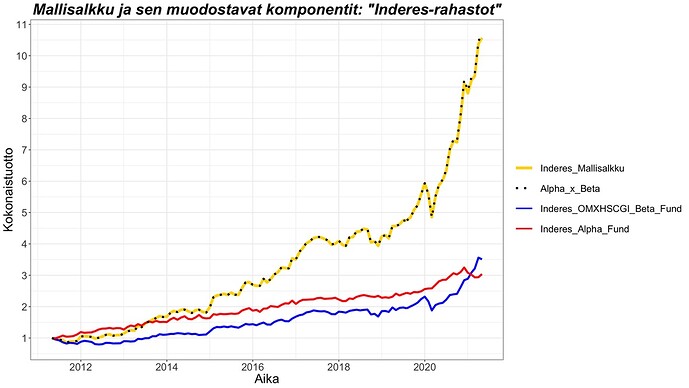
Parhaan mallin (malli #3) mukaan mallisalkun tuotto siis muodostuu mallisalkun indeksialtistuksesta sekä selittämättömästä (yli)tuotosta eli alfasta. Muodostan kaksi kuvitteellista ”rahastoa”: 1) ”Inderes_OMXHSCGI_Beta_Fund” joka on sama kuin edellisen kuvan ”OMXHSCGI_Beta” ja 2) ”Inderes_Alpha_Fund”, joka muodostetaan kuukausittaisista ylituotoista (kuukausitasolla ”Inderes_Alpha_Fund” tuotot lasketaan: ”Inderes mallisalkku” - ”Inderes_OMXHSCGI_Beta_Fund”). ”Inderes_OMXHSCGI_Beta_Fund” vastaa konservatiivista rahastoa, jolla on 79% sijoitettuna OMXHSCGI indeksiin ja 21% riskittömään korkoon. ”Inderes_Alpha_Fund” korrelaatio ”Inderes_OMXHSCGI_Beta_Fund” kanssa on tasan nolla. Alpha fundia voidaan ajatella ikään kuin hedge fundina, joka ei korreloi osakemarkkinan kanssa, mutta tuottaa merkittävästi.
Alla olevassa kuvassa esitetään nämä kaksi kuvitteellista ”Inderes-rahastoa” mallisalkun kokonaistuoton muodostavana kahtena komponenttina. Kuvasta nähdään miten kertomalla näiden kahden kuvitteellisen rahaston kokonaistuotot (mukaan lukien sijoitettu alkupääoma) keskenään saadaan aproksimoitua tarkasti mallisalkun kokonaistuotto. Esimerkiksi periodin lopussa ”Inderes_OMXHSCGI_Beta_Fund” kokonaistuotto on noin 3.5 (250% arvonnousu) ja ”Inderes_Alpha_Fund” kokonaistuotto on noin 3. Kun kerrotaan 3*3.5 saadaan noin 10.5 eli mallisalkun kokonaistuotto. Tämä kuvastaa hyvin, miten alfa eli ylituotto ikään kuin vivuttaa mallisalkun indeksituottokomponenttia (OMXHSCG altistusta). Tämä selittää miten mallisalkun tuotto on ”kammettu” alfan avulla maltillisesta indeksialtistuksesta omiin korkeuksiinsa. Kuulostaa hienolta, mutta sama pätee valitettavasti myös toiseen suuntaan: jos alfa on negatiivinen (kokonaistuotto alle 1), niin alfa vivuttaa markkinariskialtistuksen suomaa tuottoa alaspäin.
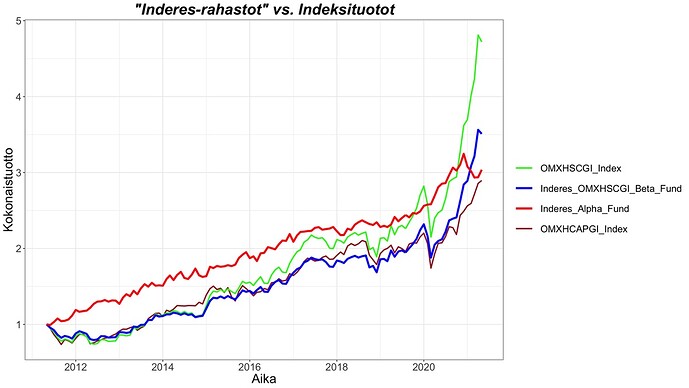
Seuraava kuva näyttää ”Inderes-rahastojen” tuotot tarkemmin verrattuna osakeindekseihin. Molempien ”rahastojen” tuotot olisivat hyvin verrannollisia osakeindeksien tuottoihin jo yksinään. ”Inderes_OMXHSCGI_Beta_Fund” seuraa tarkasti OMXHSCGI indeksin liikkeitä, mutta pienemmällä painolla. ”Inderes_Alpha_Fund” tuottoa eli mallisalkun ylituottoa on hyvä tarkastella kuvasta ajan funktiona. Ensimmäinen huomio on ylituoton tasainen nousu ajan yli. Nousu on suorastaan murhaavan tasaista pois lukien 2021 tammikuussa alkanut pieni syöksy (syöksy ajoittuu muuten samaan aikaan kun markkina meni ”erikoiseksi” Gamestoppeineen ja muine vedätyksineen. Voi toki olla sattumaakin). Tämä havainnollistaa paremmin kuin regressioanalyysin numerot, että mallisalkun ylituotto on syntynyt tasaisesti ajan yli, ei yksittäisenä tai yksittäisinä suurina nousuina. Tämä tasaisuus on iso tekijä, jotta ylituotto on niin tilastollisesti merkittävä. Toinen merkittävä huomio kuvasta on, että vaikka ylituoton korrelaatio markkinatuoton kanssa koko ajan yli on nolla, niin korrelaatio on markkinan isoissa laskuissa negatiivinen. Ylituotto on siis suojannut mallisalkkua osakemarkkinan paksun hännän heilahduksilta. Indeksit kokivat ison laskun heti mallisalkun historian alussa, mutta ylituotto suuntasi tasaisti ylös. Samoin koronakriisin jyrkässä syöksyssä ylituotto meni jyrkästi vastakkaiseen suuntaan.
Kaikki neljä kuvan ”rahastostoa”/indeksiä tuottaa karkeasti saman verran, mutta ”Inderes_Alpha_Fund” tuotto on näistä ylivoimaisesti arvokkainta. Miksi? Koska sen tuotto ei korreloi markkinariskin kanssa eli kyseessä on vaihtoehtoinen sijoituskohde korkealla tuotto-odotuksella ja matalalla riskillä – juuri sitä mitä hedge fundien pitäisi olla, mutta niin harvoin ovat. Ainoa puuttuva hedge fund komponentti on vipu, mutta siitä lisää myöhemmin.
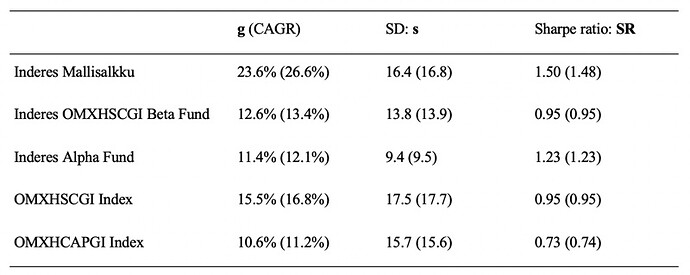
Seuraavassa taulukossa on katsaus mallisalkun, sen komponenttien eli ”Inderes-rahastojen” sekä indeksien tunnuslukuihin. Luvut on esitetty ”continuous compounding” muodossa. Suluissa on samat numerot vuosittaisilla tuotoilla (korkoa korolle vuosittain laskettuna kuten CAGR). Ensimmäisenä on portfolion vuosittainen kasvutahti (”growth rate”) g, joka usein ilmaistaan vuosittain compoundaavassa muodossa CAGR arvona1) (suluissa). Toisena portfolion volatiliteetti eli vuosittainen keskihajonta s. Ja lopuksi Sharpe ratio SR. Mallisalkun CAGR on hurjat 26.6%. Myös indeksien tuotot ovat todella kovia etenkin kun muistetaan että riskitön korko r oli surkeat 0.32% eli geometrinen riskilisä (g – r) on käytännössä lähes sama kuin g. Mallisalkun riski s on myös hyvin malitillinen. Jopa pienempi kuin small cap indeksin riski. Riskikorjatut tuotot Sharpe ratiolla mitattuna ovat kautta linjan todella kovia historiaan verrattuna. Mallisalkun Sharpe on lähes käsittämätön 1.48 (ja 1.50 cont. comb. metriikoilla). Historiallisesti pitkällä aikavälillä Sharpe on USAn indekseillä pyörinyt lähellä 0.40 tasoa eli myös indeksien Sharpet ovat lähes tuplat mitä historian valossa olisi voinut odottaa. Edelliset 10 vuotta on ollut kova bull markkina verrattain pienellä volatiliteetilla.
Syy miksi käytän metriikoita ”continuous compounding” muodossa on se, että käytän Kelly kriteeriä arvioimaan portfolion tuottopotentiaalia ja riskiä. Kelly kriteerin kaavat käyttävät metriikoita ”continuous compounding” muodossa ja antavat vastauksensa samassa muodossa. Käytännössä kaksi tärkeintä Kelly kriteerin input-metriikkaa: volatiliteetti s ja Sharpe ratio SR, joiden avulla voi laskea kaikki seuraavaksi esitettävät metriikat, toimivat hyvin myös perinteisessä (vuosittain compoundaavassa) muodossaan.
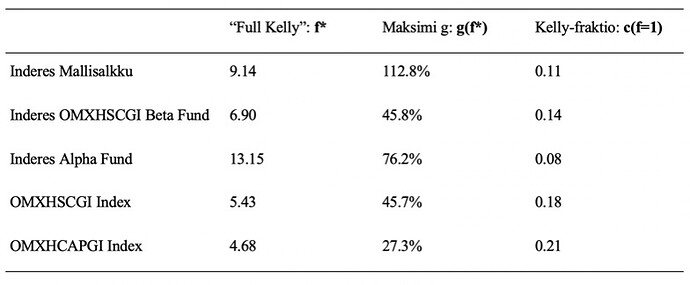
Ed Thorp on kirjoittanut tunnetun paperin Kelly kriteerin sovelluksesta osakemarkkinoille. Lisäksi olen itse tutkinut asiaa gradussani (kappale 3.3.4). Kelly kriteeri on tunnettu vedonlyönnistä, mutta se antaa näkökulmaa myös osakesijoituksiin. Portfolion geometrinen tuotto-odotus saavuttaa maksiminsa ns. ”full Kelly” sijoitusasteella f*, jonka jälkeen sijoitusasteen f nostaminen (lisävipu) alkaa pienentää geometrista tuotto-odotusta. Teoreettinen maksimisijoituspaino eli ”full Kelly” voidaan laskea yksinkertaisesti Sharpe ratio / volatiliteetti eli f* = SR/s. Portfolion teoreettinen maksimituotto eli tuotto ”full Kelly” sijoitusasteella voidaan laskea: g(f*) = SR^2/2 + r (r on riskitön korko). Ja portfolion Kelly-fraktio c saadaan ”full Kelly” käänteislukuna eli c = s/SR (”full Kelly” sijoitusasteella c = 1). Kelly-fraktio sijoitusasteen funktiona on c(f) = fs/SR.
Kelly-metriikat on laskettu alla olevassa taulukossa. Teoreettinen (tämä todellakin on vain teoreettinen yläraja, joka on hyvä tiedostaa, ei realistinen tavoite) maksimisijoitusaste mallisalkulle on hieman yli 9 (eli yli 900% sijoitusaste). Korkein maksimisijoitusaste on ”Inderes_Alpha_Fund” ja myös indeksien ”full Kelly” ovat 5 tietämillä. Historiallisesti (USAn pitkän aikavälin datasta mitattuna) osakemarkkinan ”full Kelly” on luokkaa 2 tai hieman päälle 2. Eli tämänkin metriikan perusteella olemme eläneet poikkeuksellisen hyviä aikoja markkinoilla, kun teoreettiset maksimivivut indeksitasolla ovat olleet noin kaksinkertaisia odotuksiin nähden. Myös teoreettiset maksimituotot maksimivivulla ovat tähtitieteellisiä. Kelly fraktio c kertoo kuinka suuri osuus (0 – 1) portfolion geometrisesta tuottopotentiaalista on käytössä. Mitä pienempi luku, sitä pienemmällä riskillä tuotto saavutetaan. Mallisalkun Kelly fraktio (100% sijoitusasteella eli kun f = 1) on hyvin pieni. Mallisalkku on operoinut noin 1/9 Kellyllä, mikä on hyvin konservatiivinen allokaatio. Kuvitteellinen ”Inderes Alpha Fund” on operoinut vielä pienemmällä riskitasolla, noin 1/13 Kellyllä. Historiallisesti (pitkällä aikavälillä USAn markkinoilla) 100% osakeindeksi allokaatio on operoinut noin 1/2 Kellyllä. 1/4 Kellyä voi jo pitää kohtuullisen konservatiivisena allokaationa.
Rahoitusteoria sanoo, että riski on volatiliteetti s. Kelly kriteeri sanoo, että Kelly-fraktio c = s/SR kuvaa riskiä. Kumpi on oikeassa? Molemmat ovat oikeassa tavallaan. Volatiliteetti kuvaa riskiä siinä mielessä, että se kuvaa tuotto-odotuksen epävarmuutta. Kelly-fraktio c kuvaa tappioriskiä (tarkemmin sanottuna Kelly-fraktio yksinään määrittää todennäköisyyden sille, että portfolion arvo on joskus tulevaisuudessa alle sijoitetun alkupääoman). Mitä suurempi c, sitä todennäköisemmin ja syvemmälle portfolion arvo joskus painuu tappiolle. Kelly-fraktio ottaa huomioon portfolion tuotto-odotuksen (tappio)riskiä alentavan tekijänä. Intuitiivisesti on helppo ymmärtää, että mitä suurempi tuotto-odotus, sitä epätodennäköisemmin suurehkokin volatiliteetti painaa portfolion tuottoa (esimerkiksi vuositasolla) miinukselle. Jos tuotto ei mene miinukselle, portfolion arvo kasvaa ja tappioriski ei realisoidu, vaikka riski volatiliteetilla mitattuna voi olla suurikin.
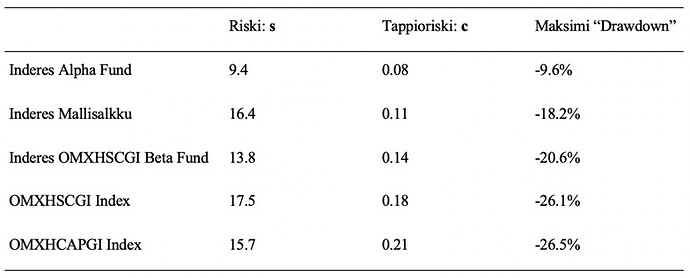
On oletettavaa, että portfolion kokemat ”drawdownit” eli kumulatiivinen tappiotuotto edellisestä portfolion huippuarvosta korreloi tappioriskin kanssa. Alla olevasta taulukosta näemme, että kymmenen vuoden maksimi ”drawdown” todella korreloi tappioriskin c, ei volatiliteetin s kanssa. Esimerkiksi OMXHCAPGI indeksin volatiliteetti on pienempi kuin mallisalkun, mutta maksimi ”drawdownit” ovat -26.5% vs. -18.2%. Kelly-fraktiolla eli tappioriskillä mitattuna mallisalkku on huomattavasti pieniriskisempi verrattuna molempiin indekseihin ja jopa verrattuna konservatiivisella 79% small cap indeksipainolla ja siten pienellä volatiliteetilla operoivaan beta fundiin. ”Inderes_Alpha_Fund” on ylivoimaisesti pieniriskisin molemmilla mittareilla.
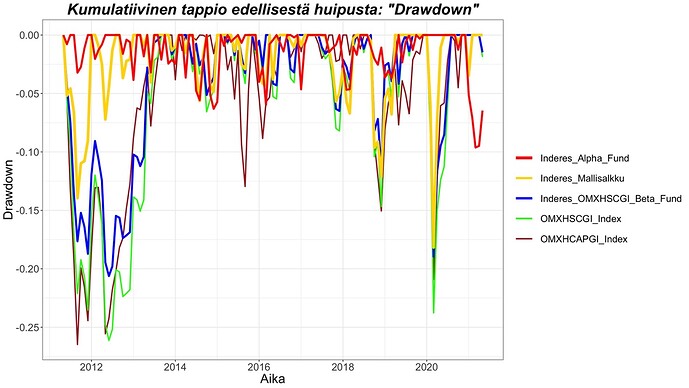
Alla näkyvästä ”drawdown” kuvasta näemme, että ei pelkästään maksimi ”drawdown”, vaan myös tyypillinen ”drawdown” on mallisalkulla selvästi pienempi kuin indekseillä. Ja että ”Inderes_Alpha_Fund” tyypillinen ”drawdown” on todella pieni.
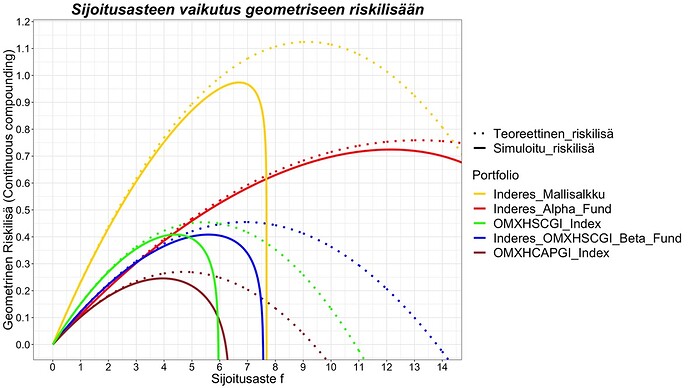
Mallisalkulla on historiansa läpi ollut käsittääkseni kohtuullisen suuri käteispositio eli selvästi alle 100% osakepaino. Seuraavaksi tarkastelemme teoreettisesti ja simuloimalla historiadatasta, miten sijoitusaste vaikuttaa geometriseen tuotto-odotukseen. Tarkemmin sanottuna tarkastelemme geometrista riskilisää (g – r) josta saadaan geometrinen tuotto-odotus lisäämällä siihen riskitön korko r.
Kelly kriteerin mukaan (tai yleisemmin geometrisen keskituoton määrittävien matematiikan lakien mukaan) geometrinen tuotto-odotus on alaspäin aukeavan paraabelin muotoinen sijoitusasteen funktiona. Tämä poikkeaa finanssiteoriasta, joka käyttää aritmeettisia tuotto-odotuksia, jotka puolestaan nousevat lineaarisesti kohti ääretöntä sijoitusasteen nousun mukana. Oikean elämän sijoittajat kasvattavat varallisuuttaan korkoa korolle ilmiön avulla ajan yli ja siksi mittaavat geometrisia tuottoja, joten on mielekkäämpää tarkastella sijoitusasteen ja vivun vaikutusta niihin. Teoreettisen paraabelin (pisteviivalla alla olevassa kuvassa) huippu osuu ”full Kelly” sijoitusasteelle f* (tai vaihtoehtoisesti c = 1). Kun mennään yli ”full Kelly” pisteen (c > 1), niin tuotto-odotus alkaa laskea samalla kun riski kasvaa. Lopulta (f > 2f* tai c > 2) päädytään odotusarvoiseen ”ruiniin” eli tuotto-odotus kääntyy negatiiviseksi. Teoreettinen geometrinen tuotto-odotus voidaan laskea mille tahansa sijoitusasteelle kätevästi: g(f) = fs(SR – fs/2) + r.
Tämä siis teoriassa. En voi korostaa liikaa, että teoreettiset käyrät ovat teoreettisia ylärajoja. Oikeassa elämässä sijoitusasteen ja vivun rajat ja mahdollinen ”ruin” tulevat monesta syystä johtuen vastaan nopeammin. Ensinnäkin Kelly kriteeri olettaa, että lainaa saa riskittömän koron hinnalla (mikä tietysti ei pidä paikkaansa). Lisäksi teoreettinen käyrä olettaa, että sijoittaja rebalansoi takaisin tavoitesijoitusasteeseen äärettömän tiheään. Kuvassa simuloidut käyrät käyttävät kuukausittaisia tuottoja eli kuukausittaista rebalansointia takaisin tavoitepainoon. Erityisesti suurella vivulla rebalansointi pitäisi suorittaa tiheään. Ja tietysti margin call tulee käytännössä paljon aikaisemmin kuin pääoma menetetään. Lisäksi on varmaan paljon muita käytännön syitä (joista en tiedä, koska en ole itse ottanut vipua ja joutunut siten selvittämään riskejä tarkemmin) miksi vipu tappaa mahdollisesti aikaisemmin kuin teoreettiset käyrät ennustavat. Oleellista on kuitenkin huomata, että rahoitusteoriassa (aritmeettisilla tuotoilla) vivun ylärajaa ei aseta mikään muu kuin sijoittajan riskinsietokyky. Oikeassa elämässä geometrisilla tuotoilla operoitaessa matematiikan lait asettavat ylärajan riskinsietokyvystä riippumatta.
Kuvasta nähdään, että mitä pienempi Kelly-fraktio eli tappioriski c portfoliolla on, niin sitä paremmin portfolio sietää vipua. Erityisesti nähdään, että pienimmän Kelly-fraktion omaava ”Inderes_Alpha_Fund” sietää vipua myös simulaatiossa (jossa käytän siis historiallisia kuukausituottoja ja vivutan niitä) lähes yhtä hyvin kuin teoria ennustaa. Mallisalkku kestää aikansa teoreettisen käyrän mukana, mutta sitten noutaja tulee nopeasti ja yllättäen. Kohtisuora tiputus käyrässä tarkoittaa, että kuukauden aikana koko pääoma pyyhkiytyi pois, jolloin ei jäänyt enää mahdollisuutta rebalansoida velkapositiota. Äärimmäistä vivuttamista voisi simulaatiokäyrien perusteella kuvata klassikosta muokatulla sanonnalla: ”Picking up fortunes in front of a steamroller”. Suuri tuotto-odotus, suuri äkkikuolemanvaara.
Simuloiduista käyristä nähdään myös, että simuloitu mallisalkun käyrä tulee hyvin nopeasti alas, kun mallisalkun osakemarkkina-altistus ”Inderes_OMXHSCGI_Beta_Fund” tulee alas. Paksuhäntäinen markkinariski dominoi äkkikuolemanvaaraa ja ainakin kuukauden rebalansointitaajuudella ylituotto ei suurella vivulla juuri pysty suojaamaan mallisalkkua äkkikuolemalta.
”Inderes_Alpha_Fund” vivunsietokyky antaa ymmärtää, että tälle kuvitteelliselle rahastolle voisi soveltaa vielä sitä yhtä hedge fundien ominaisuutta eli vipua. 2x vivulla meillä olisi edelleen kohtuullisen (vajaan 19 prosenttiyksikön) volatiliteetin omaava rahasto yli 20% tuotto-odotuksella ja nollakorrelaatiolla markkinaan.
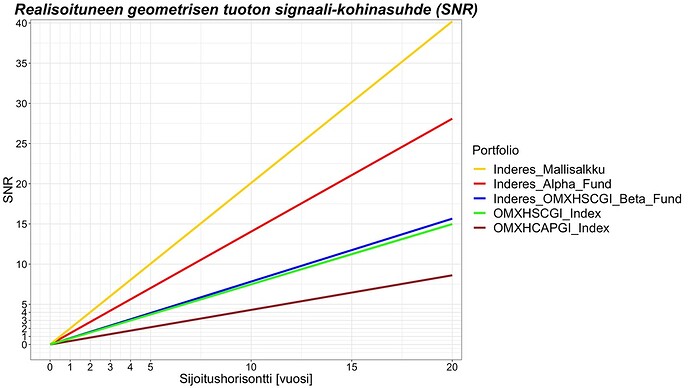
Usein kuulee sanottavan, että osakemarkkinoilla on paljon kohinaa tai että tuotot ovat kohinaisia. Vaikka kohinasta tai ”noisesta” puhutaan paljon, sitä ei yleensä määritellä tarkasti tai ainakaan niin että määritelmä olisi universaalisti sovittu ja sama. Me voimme kuitenkin lainata määritelmän kovista insinööritieteistä. Signaalinkäsittelyssä tärkein yksittäinen metriikka on signaali-kohinasuhde ”Signal to Noise Ratio” eli SNR. SNRn määritelmä on signaalin teho jaettuna kohinan teholla. Voimme ajatella portfolion geometrisen riskilisän g – r signaalina ja sen epävarmuuden eli volatiliteetin (tai keskihajonnan) kohinana. Tällöin realisoituneen portfolion geometrisen riskilisän Signaali-kohinasuhde SNR = (g – r)^2/s^2 eli portfolion riskilisän neliö jaettuna portfolion varianssilla. Jos esitämme kaavan jälleen Sharpe ration, volatiliteetin, sijoitusasteen ja nyt myös ajan funktiona, se voidaan kirjoittaa: SNR(f, t) = t(SR – fs/2)^2 (t on aika vuosina. SNRn ominaisuus on, että se skaalautuu suoraan verrannollisesti aikaan). Alla näkyvässä kuvassa olen plotannut eri portfolioiden SNRt ajan funktiona. Edellisellä 10 vuoden periodilla riskitön korko oli käytännössä nolla (0.32%) eli geometrinen riskilisä oli käytännössä sama kuin geometrinen tuotto.
Kuvasta nähdään, että mallisalkun SNR on poikkeuksellisen korkea. Vuoden periodilla se on jo 2 eli kaksi kertaa enemmän signaalia kuin kohinaa. Jos ajattelemme minimisijoitushorisontin aikana, joka vaaditaan, jotta tuotto-odotus alkaa dominoida realisoituvia tuottoja kohinan sijaan, tarkoittaa se, että ajan täytyy olla riittävän pitkä, jotta SNR > 1. Mallisalkulle tämä SNR = 1 saavutetaan jo puolen vuoden sijoitushorisontilla. 10 vuoden sijoitushorisontilla mallisalkun realisoituneen riskilisän SNR on jo 20. Myös indeksien SNRt ovat poikkeuksellisen korkeita. Esimerkiksi OMXHCAPGI indeksi vaatii vain 2.3 vuotta saavuttaakseen SNR = 1 tason. Vertailun vuoksi USAn markkinoilla (”equally weighted”) markkinatuotto vaati periodilla Jan/1973 – Jun/2018 keskimäärin noin 7 vuotta saavuttaakseen tuon minimisijoitushorisontin. Tässäkin suhteessa olemme eläneet poikkeuksellisen suotuisat edelliset 10 vuotta.
Yhteenvetona analyysin tarjoamat vastaukset alussa esitettyihin kysymyksiin:
-
Mitkä rahoitustutkimuksesta tutut riskifaktorit selittävät mallisalkun tuottoja ja selittyykö mallisalkun suuri tuotto riskifaktoreilla eli sijoitustyylillä?
Markkinatuoton lisäksi vain size factor selittää pienen osan tuotoista.
Hyvin suuri osa mallisalkun tuotosta jää selittämättä sijoitustyylillä -
Mikä on paras (mallisalkun tuottoja ja riskejä parhaiten kuvaava) vertailuindeksi?
Helsingin small cap indeksi OMXHSCGI -
Onko mallisalkulla tilastollisesti merkittävää ylituottoa (alfaa) kun mallisalkun tuotot selitetään vertailuindeksin tuotoilla?
On. Tilastollisesti erittäin merkittävä alfa: p-arvo = 3.010050e-04. -
Onko mallisalkulla tilastollisesti merkittävää ylituottoa, jos huomioidaan indeksin lisäksi videollakin mainitut mallisalkun paras osake Revenio tai parhaat neljä osaketta?
Kyllä. -
Mistä pääkomponenteista mallisalkun tuotto muodostuu?
OMXHSCGI indeksialtistus (beta 0.79) ja ylituotto eli alfa. -
Kuinka suurella riskillä mallisalkun tuotto on saavutettu?
Riski on yllättävän pieni. Volatiliteetti on maltillinen ja tappioriski hyvin alhainen. -
Osakepaino on ollut reilusti alle 100%. Miten ja millaisella riskillä salkku olisi tuottanut suuremmalla osakepainolla?
Simulaation perusteella mallisalkku olisi kestänyt hyvin vipua. Tuotot olisivat olleet hyvin korkeita riippuen vivusta. En lähde suosittelemaan vipua, mutta mikäli Inderesillä ei ole lähes yliluonnollista ajoitustaitoa, on vaikea nähdä juurikaan alle 100% osakepainoa järkevänä näillä parametreilla (tai edes jonkin verran huonommilla parametreilla). -
Onko tuotto ja mahdollinen ylituotto ollut taitoa vai tuuria?
10 vuoden periodilla mallisalkun realisoituneen kasvunopeuden signaali-kohinasuhde SNR = 20. Mallisalkun realisoituneessa kasvunopeudessa (g = 23.6% eli CAGR = 26.6%) voidaan siis sanoa olevan noin 20 kertaa enemmän tuotto-odotuksen kuin sattuman vaikutusta.
Todennäköisyys, että Inderesin mallisalkun hoitajilla ei ole sijoitustyylistä puhdistettua osakepoimintataitoa ja mallisalkun ylituotto toteutuu vähintään yhtä merkittävänä kuin se nyt on toteutunut on p-arvon mukaan 1/3322. Eli todennäköisyys jäädä ylituoton tilastollisessa merkittävyydessä alle mallisalkun tason olisi ilman osakepoimintataitoa noin 99.97%.
Vaikka huomioimme salkun neljä parasta sijoitusta mallisalkun tuottoa selittävinä tekijöinä small cap indeksin lisäksi, mallisalkun ylituotto on edelleen tilastollisesti merkittävä ja suuri. Ylituottoa on syntynyt laajalla rintamalla.
→ Näiden numeroiden valossa kyse on taidosta, ei tuurista.
Yritin analyysissä parhaani mukaan selittää mallisalkun riskin ja tuotot faktorimallien avulla. En onnistunut tässä kovin hyvin. Olettaen, että en tehnyt suurempia virheitä analyysissä tai jättänyt olennaisia faktoreita mallin ulkopuolelle, syy epäonnistumiseeni on se, että merkittävää osaa mallisalkun tuotoista ei voi selittää muuten kuin onnistuneella osakepoiminnalla.
1) CAGR = exp(g) – 1, g = ln(1 + CAGR)